Example 10: Mixture Surface Design
Cornell (1990a) discusses a simple but typical mixture experiment concerned with the average texture of fish patties. Sandwich patties were made of blends of three types of fish: Mullet, Sheepshead, and Croaker. The dependent variable of interest was Texture, as measured by the force (in grams * 10-3) required to puncture the patty surface. The experiment, as reported by Cornell (1990a, page 9), used a second-degree simplex-lattice mixture design. Experimental designs for mixtures are also discussed in detail in the Introductory Overview in the Experimental Design module.
- Specifying the analysis
- The data discussed by Cornell (1990a) are contained in the example data file Fish.sta, and we will first perform an analysis using a main-effects only model.
Ribbon bar. Select the Home tab. In the File group, click the Open arrow and select Open Examples to display the Open a STATISTICA Data File dialog box. The Fish.sta data file is located in the Datasets folder. Then, select the Statistics tab. In the Advanced/Multivariate group, click Advanced Models and from the menu, select General Linear to display the General Linear Models (GLM) Startup Panel.
Classic menus. From the File menu, select Open Examples to display the Open a STATISTICA Data File dialog box. The Fish.sta data file is located in the Datasets folder. Next, from the Statistics - Advanced Linear/Nonlinear Models submenu, select General Linear Models to display the General Linear Models (GLM) Startup Panel.
Select Mixture surface regression as the Type of analysis, Quick specs dialog as the Specification method, and then click the OK button to display the GLM Mixture Surface Regression Quick Specs dialog box.
Click the Variables button to display the standard variable selection dialog box. Select Texture from the Dependent variable list. Select Mullet, Sheepshead, and Croaker as the Predictor variables. Then, click the OK button to return to the GLM Mixture Surface Regression Quick Specs dialog box.For this example, we can estimate the pure error and test for overall lack of fit. Lack of fit tests require the computation of the pure error not accounted for by the model. To specify the computation of the pure error, select the Options tab. In the Parameterization group box, select the Lack of fit check box.
Note: the No intercept check box is automatically selected. Mixtures, as the name implies, add up to a constant value; the sum of the proportions of ingredients in different recipes for some material all must add up 100%. Thus, the proportion of one ingredient in a material is redundant with the remaining ingredients. Mixture surface regression designs deal with this redundancy by omitting the intercept from the design.Because the default mixture surface design includes terms in addition to main effect terms, we can modify the analysis specifications in the syntax editor. Click the Syntax editor button to display the GLM Analysis Syntax Editor. In the Analysis syntax field, the DESIGN statement for the default full quadratic response surface design will be:
DESIGN = MULLET | SHEEPSHD | CROAKER @2;
Edit the DESIGN statement so that it specifies a main effects only model:
DESIGN = MULLET + SHEEPSHD + CROAKER;
The complete syntax specifications for the analysis should now be:
Now click the OK (Run) button to begin the analysis.
Reviewing Results.
- Lack of fit tests
- The
GLM Results dialog box will be displayed when the analysis is complete. To obtain a test of
lack of model fit, click the Whole model R button under Between effects on the
Quick tab. The Test of Lack of Fit spreadsheet will show the following results.
The Lack of fit test is marginally significant (p<.10), suggesting that the simple linear main-effects-only model is too simple.
Now, modify the analysis by specifying the default quadratic mixture surface design. In the GLM Results dialog box, click the Modify button to return to the GLM Analysis Syntax Editor. In the Analysis syntax field, change the DESIGN statement to read:
DESIGN = MULLET | SHEEPSHD | CROAKER @2;
Then click the OK (Run) button to run the modified analysis. When the GLM Results dialog box is displayed, click the Whole model R button again.
Note: the lack-of-fit test cannot be computed for this design. This is because the second-degree mixture model exhausts all information that can be estimated from this second-degree simplex-lattice design. - Test of whole mixture model
- The results in the Test of Whole Mixture Model spreadsheet show that the second-degree mixture model is highly significant, p < .001. Note that the degrees of freedom for the whole mixture model test (df Model) of 5 is one less than the 6 effects in the design, i.e., the 3 main effects plus the 3 two-way interactions. This is because the whole mixture model test is adjusted for the mean, which results in the loss of a degree of freedom for the test; see also the discussion of mixture designs and triangular surfaces in Experimental Design). For various other alternative ways for computing the R-square value, refer to Kvalseth (1985).
- Regression coefficients
- On the
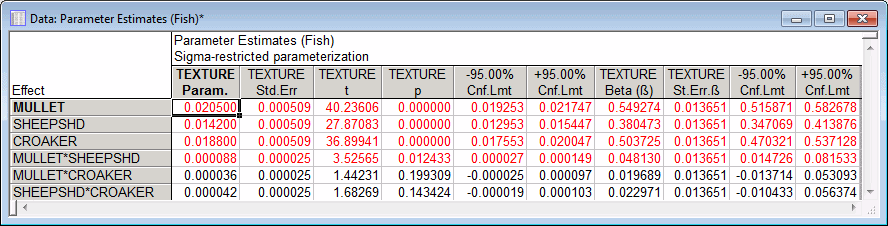
Summary tab of the GLM Results dialog box, click the Coefficients button to produce the Parameter Estimates spreadsheet for the coefficients for the regression equation.
As can be seen, the coefficients for every effect except Mullet*Croaker and Sheepshd*Croaker are significant. Note, however, that the coefficients for main effects should be interpreted with caution due to the exclusion of the intercept term from the model.