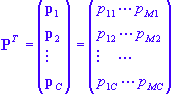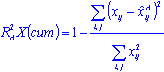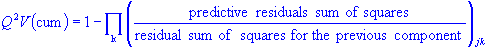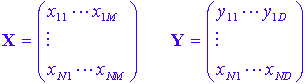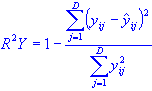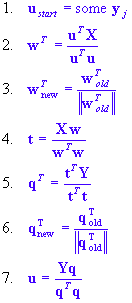NIPALS Technical Notes

Principal Component Analysis

The aim of the Principal Components Analysis (PCA) is to reduce the dimensionality of a set of M variables while retaining the maximum variability in terms of the variance-covariance structure. In other words, PCA tries to explain the variance-covariance structure of a data set using a new coordinates system that is less in dimension than the number of original variables. Given a set of variables, say X, a PCA model transforms these variables into a new set, say , with the new coordinates system that has a fewer number of dimensions, i.e., C < M, and yet can capture most of the variability in the original data set. Each coordinate in the new transformed system is known as a principal component and, hence, the name Principal Component Analysis.

PCA is a technique of great practical importance in many applications of statistical inference, most notably when we are faced with the problem of relating a large number of independent variables with a number of dependent outcomes without having enough observations to carry out the analysis in a reliable way. In such cases, there is seldom enough data to make reliable inference due to the curse of dimensionality (Bishop 1995) resulting from the large dimensionality of the problem, i.e., the large number of the predictor variables. The PCA method alleviates this problem by mapping the original predictors into a set of new variables known as principal components. Such a transformation will usually be accompanied with a loss of information. The goal of PCA, therefore, is to preserve as much as information contained in the data as possible. The optimal number of PCs (principal components) needed to achieve this task is not known a priori. The criterion here is to find a set of C principal components with eigenvalues that have a significantly larger value than the remaining M – C. This procedure requires the definition of a threshold for the retrieved eigenvalues beyond which the rest of the PCs are regarded to be insignificant. In other words, we discover an effective number of transformed variables that explains the original data best. This is known as the intrinsic dimensionality.

Following a PCA model, we hope to be able to interpret the first few principal components in terms of the original variables, and thereby have a greater understanding of the data. However, like many methods in statistical inference, PCA requires a pre-processing stage in which the original variables are transformed in a way that the general assumptions about the data set will hold best. This is known as pre-processing.

Pre-processing. In multivariate analysis, variables often have substantially different ranges (i.e., different variances). This may have to do with the units of measurements or simply the nature of the variables. However, the numeric range of a variable, among many, may not be a good indication of how important that variable is.

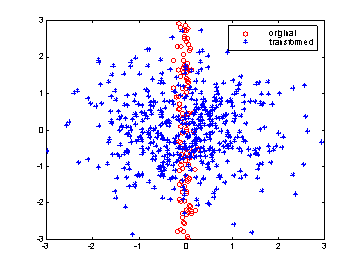
The above illustration shows the scatterplot of a simple multivariate data set consisting of two variables. Due to differences in scaling, an immediate visual inspection of the original observations (the red circles) provides us with the false impression that most of the variability in the data comes from the second dimension, X2. However, if we rescale the variables appropriately, it will instantly become clear that variable X1 adds as much variability to the data set as X2 (the blue points). Thus, it is always necessary to rescale variables of a multivariate data set in a way that no variable adds superficial variability to the problem just because of its scale.

As we saw above, the unit of measure may add some superficiality to the data that needs to be eliminated for various reasons. For example, in statistical modeling, such variables can bias predictions leading to bad models. More specifically, since in PCA the original variables are represented in a fewer number of dimensions while preserving maximum variability, it is clear that variables with larger ranges will be more represented in the data than others. This superficial influence often leads to faulty models. That is why scaling is so crucial in multivariate analysis.

Mean centering and unit variance

There are several ways of scaling the observations of a data set X, the most popular of which is unit variance scaling. Here, every variable of the data set is transformed in a way such that the new variable has unit variance, thus providing equal chance to all variables for representation by the PCA model.

Another form of pre-processing is mean centering, which involves defining a new point of origin for the data defined by the multivariate mean. It provides a convenient new point of reference for the transformed variables from which further analyses can be carried out (see schematic below).

Mean centering and unit variance scaling are actually applied in one single step in the form of a linear transformation defined as:

Using appropriate mathematical notation we can rewrite the above as:

with

where 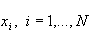is a typical observation of the variable Xi, with and 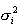as its mean and variance, respectively. It is easy to show that the above linear scaling, also known as soft scaling, will transform the original variable 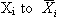with zero mean and unit standard deviation.

In summary, scaling transforms variables of a multivariate data set in a way such that the variables become comparable on equal footings, thus preventing variables with larger values from dominating those with smaller ranges and, hence, eliminating over representation of some variables merely on the basis of size. Equally important, mean centering will provide a new point of origin that can help with interpreting the model.

PCA Revisited

Data pre-processing can be looked at, in many ways, as an integral part of PCA. While scaling helps to treat all variables on the same level, centering makes the interpretation of the model easier. After pre-processing, the next step is to find a number of principal components that represents the original variables X best in the least squares sense. In other words, we find a new coordinate system set that predicts a matrix of observations 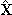as an approximation to X. This step is carried out incrementally; we start with extracting the first principal component, i.e., the principal component that captures the largest portion of variability in X. Then we continue finding more components until we reach a point where the extracted principal components capture a certain percentage of variability in the data set (for more details, see The NIPALS algorithm for PCA below).

PCA in one dimension (a toy model)

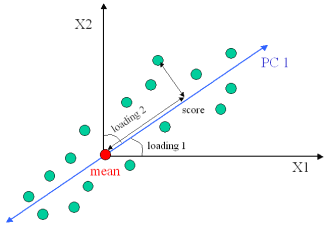
Now we will consider the simplest form of a PCA model, consisting of a single principal component. Without loss of generality, let's assume for now that our data X is bivariate, i.e., contains only two variables. Such data can be represented using a single principal component, i.e., C=1, which we denote by PC1. A schematic diagram for PC1 is shown in the figure below, where we can see that PC1 (a line) is passing through the mean of the multivariate data set X. Thus, by mean centering of X as part of the pre-processing step, we in effect created a point of origin for the new coordinate system (which in this case is defined by PC1). The orientation of PC1 is chosen in such a way that it captures maximum variability in the data. Each observation in the original data set xi = (x1, x2) can now be projected onto PC1. This projection along PC1 is known as the score ti. In other words ti is the new value of an observation in the new coordinate system. Thus, for a data set X with N observations, the score vector t = (ti,...,tN) uniquely defines the transformed data set.

A schematic of a toy model consisting of 2-dimensional data represented by a single PC. The "mean" of the original data set serves as the point of origin for the principal component. The transformed value of an observation in X is given by its score, which simply measures its distance from the origin along PC1. Note that the orientation of PC1 is completely determined by its angles (loading factors) with respect to the old coordinate system.

The line defining PC1 takes its orientation with respect to the original variables in a way that it captures maximum variability in the data. The cosine of the angle between this line and a variable xi is known as the loading factor. It measures how well a variable loads into PC1, i.e., how much variable xi contributes to the PCA model. Thus, given a set of M original variables, 2 in this case, the vector p = (p1 p2) uniquely defines the orientation of PC1 with respect to the original coordinate system.

Extension to multiple dimensional PCA

In the previous section, we assumed that the data set X can be expressed by a single principal component PC1. Depending on the dimensionality of X, however, this is often not the case. In most applications more than one principal component is needed to adequately capture the variability and, hence, the information in the data set.

In the simpler case of a two dimensional PCA model, this projection is a point in the plane defined by PC1 and PC2. More generally, PCA models find hyper-planes in C dimensions that approximate the data set best. Note that in the new representation of the data set, the principal components are orthogonal, i.e., the angles between a component and the rest are 90 ° .

For multi-dimensional PC models, the set of principal components forms an orthogonal system with point of origin given by the mean of the original data set and orientation defined by the loading factors,

where C is the number of PCs in the model and M is the number of variables in X.

While the matrix P defines the principal component's scores, matrix T defines the representation of the original observations in the new coordinate system:

Using the above, the predictions 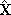of the PCA model for the pre-processed data set 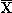is then given by .

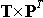The mathematical model

In this section we will look into some mathematical details of constructing the PCA model. Here we consider the representation of the original data set X with the aid of a number of principal components with dimension C which is smaller than the number of variables M in X. In matrix notation this representation can be written as:

= + E

where 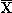is the preprocessed data and 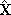is the predictions of the PCA model. The noise matrix E gives the residuals, i.e., differences between 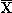and the predictions ,

E = X –

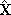The matrix 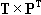can also be written in terms of their vector components:

An algebraic representation of the PAC model.

The loading factors are arranged in the order of the largest eigenvalues of the covariance matrix XXT.

At least in principle, the more components we add to a PCA model, the smaller the elements of the matrix E should become. As we will see shortly, the matrix of residuals E plays an important role in detecting outliers that might be present in the data set X. A feature that can be used effectively for data inspection and diagnostics.

The N x C dimensional matrix T contains the scores of the principal components in the new coordinate system. In other words, it consists of the coordinates of the original observations in the PCA model. It is customary to arrange the scores such that t1 belongs to the principal component PC1, which captures variability more than t2, t3, ..., tc.

T = (t1,..., tc)

The matrix loading factors matrix:

P = (p1,..., pc)

has dimensions M x C and contains the loading factors of the principal components, which, geometrically, determine the orientation of the principal component with respect to the original coordinate system and, algebraically, determines how well a variable will contribute to forming the scores. They also indicate how correlated the original variables are as we shall discuss later.

Data diagnostic using the PCA model

In the previous sections, we learned that by just considering the loading factors and the scores we can shed light on the importance of the original variables and their correlations, which can be used as a diagnostic tool for model interpretation. One more such tool offered by PCA is the residuals (mentioned in the previous section). Again we reiterate that by residual we mean the difference between the 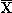data set and the predictions of the PCA model, which we denote by 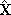. In other words, residuals are that part of 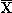that is not captured by the principal components.

One of the advantages of PCA is its ability to diagnose the data on both observation and variable levels (Wold et al 1984 and Wold et al 1986). This diagnostic capability is inherent in the mathematical model of PCA and can be utilized without further assumptions. Diagnostics on observation level helps us to detect and identify outliers, which may be an indication of abnormalities. This plays an important role in process monitoring and quality control. On the other hand, diagnostics on the variable level helps us to decide how well the variables are represented by the principal components, the way they relate to each other, and their contributions to building the PCA model.

Outliers are observations that do not well fit the normal trend in the data set. Strong outliers are detected by the value of their x-scores since they have the ability to pull the model toward themselves, and moderate outliers are identified using the residuals. One way of visualizing strong outliers is the Hotelling T2. T2 for observation i is given by:

where tik is the score of the ith observation for the kth component and is the estimated variance of tk. Note that ensures that each PC has an equal chance in calculating T2.

The Hotelling T2 is not sufficient for predicting outliers, especially with new observations, i.e., observations that were not present in the data set used to train the model. A better quantity is the Square of the predictions error - SPE (MacGregor and T. Kourti). For the ith observation SPE is defined as:

where xij and 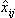are the elements of 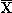and 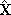, respectively.

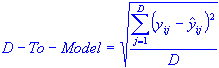
Moderate outliers do not have the power to pull the model toward themselves and cannot be easily detected with the Hotelling T2. An alternative approach is offered by the residuals (i.e., matrix E). The residuals are used to detect the so-called distance to model (D-To-Model). A data case is labeled as an outlier if the corresponding value of its distance to model is found to exceed a given threshold value. For a typical observation i, the distance to the model is calculated as:

where the freedom DF is defined as the difference between the number of variables in X and the number of principal components,

 DF = M – C

The elements of the residual matrix E can also be used for data diagnostics on the variable level. For example, the importance of a variable is based on how well it is represented by the PCA model. This is measured by the modeling power, which is defined as the explained standard deviation.

where SVj is the residual standard variation of the jth variable and 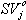is its initial standard deviation. Note that unit scaling 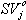is equal to  unity for all variables in 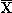. A variable is completely relevant if its modeling power is equal to 1. Variables with low modeling power are of little relevance.

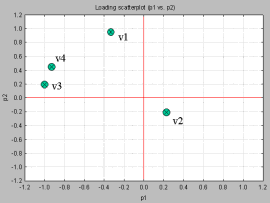
Note: variable importance in PLS is similarly computed, except that the proportion of variability explained in the X variables is further weighted by variability accounted for by the components. This index is often called VIP (Variability Importance in the Projection), and is described below.

One of the useful diagnostic tools for exploring the role of the variables and their contribution to the PCA model is the scatterplot of the principal components. The following schematic shows the scatterplot of PC1 and PC2 for a PCA model for 5 variables.

The fact that variables v3 and v4 are close (in the upper left section) means that they influence the PCA model in similar ways. It also means that they are positively correlated. v2 also contributes to the PCA model in ways similar to those of v3 and v4. The further a variable is away from the origin, the more influential that variable is. This means that v2 is less influential compared to the rest. This variable is also negatively correlated to v1, v3, and v4 (since it is positioned diagonally opposite of the upper-left quadrant where v3 and v4 is). This simply means that v2 contributes to the PCA model in ways different from v1, v3, and v4.

Other quantities useful for PC model diagnostics are the fraction of the explained variation R2X and the fraction of predicted variation Q2X. R2X is measured on the entire training sample using the formula:

The denominator is the residual sum of squares and the numerator is the total variation in the original pre-processed data set. For a PC model with, say, A components, the cumulative 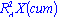is given by:

where 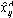is the prediction of the PC model (with A components) for the ith observation of the jth variable. Using the above expression, the explained fraction of variation due to adding the next principal component can be written as:

The more significant a principal component, the larger its R2X. In general, a PC model with a sufficient number of components will have a value of R2X (cum) close to 1.

The predictive variation Q2 is mathematically identical to R2X but it is measured using a sample of observations that was not used to construct the PC model,

Given a PC model with A principal components, Q2 (cum) is defined as:

Unlike R2X, Q2 and Q2(cum) increases as we add more and more components to the PC model. However, this trend gives way to a decrease as we add more components beyond a certain point. The point of inflation in the value of Q2 provides an estimate of C (see The Method of Cross-Validation section). Note that one can also define Q2(cum) and its cumulative for a single variable j,

Q2V explains how well a variable is represented by the principal components.

Limit and significance of a principal component. In this section, we outline a criterion for measuring the significance of a principal component that we will later use in determining the optimal complexity of the PC model using the method of cross-validation (see The Method of Cross-Validation section).

The Limit of the kth principal component is defined as the ratio of the degree of freedom DFk it consumes to the total degree of freedom of the PC model before it was added:

A principal component is regarded as significant if one of the following rules are satisfied:

1. Q2 > Limit
2. At least variables has Q2 V> Limit.
3. If neither rule 1 nor 2 is fulfilled, a component is still regarded as significant should the proceeding one satisfy either 1 or 2.

Model complexity

The primary task of PCA is the representation of the original variables with a number of principal components C which is lesser in dimension than that of the data set X, i.e., C<M. In PCA, it is fundamental to ask "how many principal components should be in the model?". In this context we can view the number of principal components as a nuisance parameter that needs to be estimated using a suitable method.

Any method used for determining C should take into account not only the goodness of fit but also the complexity taken to achieve that fit. In other words, when building PC models, we should strike a balance between the number of principal components and the ability to accurately predict data. A model with an insufficient number of components cannot predict the data accurately enough. A model with too many components has more components that it needs to predict the data.

The trade off between model complexity and the goodness of fit is deeply rooted in the principal of Occam's razor (Sir William Of Occam 1285-1349), which states that if two models with different complexities explained the data equally well, we should then favor the simpler one.

The quantity used to find the optimal complexity of a PC model is the predicted variation Q2. As we add more and more components to the PC model, Q2 increases. However, this trend gives way to a decrease in Q2 if we add more components beyond a certain point. The point of inflation in the value of Q2 provides an estimate of C.

The Method of Cross-Validation

By calculating Q2 for PC models of increasing complexity, starting from 0, we can actually find the optimal number of principal components that achieves maximum Q2. STATISTICA NIPALS Algorithm (PCA/PLS) implements this technique using either the method of v-fold or Krzanowski cross-validation.

In the v-fold cross validation, the data is divided into v segments, v-1 of which is used to build the model and the rest is used for testing. This process is then repeated for all possible permutations of the training and testing segments and the overall Q2 and Q2V are calculated for the newly added principal component using the test samples. Given the estimated values of Q2 and Q2V we can then determine, using rules 1-3 (see the Limit and significance of a principal component section), whether a principal component is significant or not.

In contrast to v-fold cross-validation, Krzanowski (Eastman and Krzanowski, 1982) does not partition the data into folds, but rather removes an entry (for all entries), one at a time, from the matrix 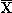.  This missing entry is treated by the NIPALS algorithm as missing data and then the model is used to predict its value, which in turn is used for calculating Q2 and Q2V and, hence, the significance of the principal component in question.

Whether using Krzanowski or the standard v-fold cross-validation, the above steps are repeated for an increasing number of principal components, starting from 0. For each extracted component, the test of significance is applied. This process is repeated until we can no longer find a significant component to add to the model.

The NIPALS algorithm for PCA. The NIPALS algorithm is an iterative procedure used for constructing PCA models for the representation of multivariate variables X using a number of principal components that are less in dimension than the number of the original variables. It is the most commonly used method for calculating the principal components and provides numerically more accurate results as compared to other methods such as the technique of decomposition of covariance.

The algorithm extracts one principal component at a time. Each component is calculated from the iterative regression of X onto the x-scores t, such that at each iteration a better loading factor p is found. The value of p is then used to improve the estimate of t.

As discussed before, we preprocess the original variables such that they have zero mean and unit (or user defined) standard deviation. This will yield the data matrix 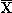, which will be used in all subsequent calculations.

1. To start the iterative procedure for extracting a component, we begin with a value of tk as the starting point. This initial value may be selected from a column of 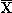with the highest remaining residuals. Again, we re-iterate that 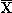is the representation of the pre-processed data.
2. Improve the estimate of the loading vector pk by projecting the Xk-1 .
   

   and normalize the length of Pi using

   
3. Improve estimate of the score tk by projecting the matrix Xk-1  on the loading vector pk.
   
4. Using the kth scores, re-estimate the eigenvalues from:
   
5. If the difference between the estimates of from two successive cycles were below a certain threshold, the algorithm has converged. If not, keep repeating steps 2 through 4.

Partial Least Squares

Partial Least Squares PLS (also known as Projection to Latent Structure) is a popular method for modeling industrial applications. It was developed by Wold in the 1960s as an economic technique, but soon its usefulness was recognized by many areas of science and applications including Multivariate Statistical Process Control (MSPC) in general and chemical engineering in particular.

It many ways, PLS can be regarded as a substitute for the method of Multiple Regression, especially when the number of predictor variables is large. In such cases, there is seldom enough data to construct a reliable model that can be used for predicting the dependent data Y from the predictors variables X. Instead, we get a model that can perfectly fit the training data while performing poorly on unseen samples. This problem is known as over-fitting (Bishop 1995). PLS alleviates this problem by adopting the "often correct" assumption that, although there might be a large number of predictor variables, the data may actually be much simpler and can be modeled with the aid of just a handful of components (also known as latent). This in fact is the same technique used by PCA for representing the X variables with aid of a lesser number of principal components.

The idea is to construct a set of components that accounts for as much as possible variation in the data set while also modeling the Y variables well. The technique works by extracting a set of components that transforms the original data X to a set of x-scores T (as in PCA). Similarly, the Y data is used to define another set of components known the y-scores U. The x-scores are then used to predict the y-scores, which in turn are used to predict the response variables Y. This multistage process is hidden and all we see, as the outcome, is that for a set of predictor variables X, PLS predicts a set of relating responses Y. Thus, PLS works just as any other regression model.

A schematic representation of the PLS model.

Just as before, both X and Y are matrices of data:

and it is assumed there exist a relationship of the form:

which relates an observation in Y to the corresponding one in X. The relationship f is not known a priori but can be modeled using PLS.

Just as in PCA, both the dependent and independent variables are pre-processed using scaling and mean centering (see pre-processing, above).

To build a PLS model, we need to regress the original data X onto the x-scores T, which are used to predict the y-scores U, which in turn are used to predict the responses Y. Thus:

where Q is the y-loadings and F is the matrix of residuals that models the noise. The above equations represent the so-called outer relations of the PLS model. In addition there is also an inner relation that results from the interdependency of Y variables on X. As we shall see later, both the outer and inner relations can be built using the NIPALS algorithm (see NIPALS algorithm for PLS, below).

Just as in all regression models, it is the aim of PLS to minimize the residuals F as much possible while also having a representation of the relationship between X and Y that generalizes well for unseen (validation) data. Because of the inner relationship, the principal components used for representing X and Y cannot be calculated separately. In other words, when building the PLS model, the outer relationships should know about each other so they cooperate in building the model as a whole, i.e., build a predictive model capable of relating X to Y. This means that the outer relations cannot be separately handled but rather treated as parts of the same problem. This condition is fulfilled by re-writing the second outer equation as:

where B is the matrix of coefficients that relates the matrix of x-scores T to the matrix of y-scores U. In essence, TB defines an inner regression problem that relates the x-scores to the y-scores. In other words, T is used to regress U. In that sense, B is merely the regression coefficients.

An algebraic representation of the PLS model.

Just as the X variables, the R2Y can also be defined for the Y variables from the fraction of the explained variance:

Just as X, you can detect outliers using distance to model defined for Y,

where D is the number of Y variables.

NIPALS Algorithm for PLS

STATISTICA PLS uses the state-of-the-art NIPALS algorithm for building PLS models. The algorithm assumes that the X and Y data have been transformed to have means of zero. This procedure starts with an initial guess value for the y-scores u and iteratively calculates the model properties in separate and subsequent steps:

If t did not change (within a certain rounding error) between two successive cycles, the algorithm has converged. After convergence is reached, the x-loading factors are calculated and normalized from 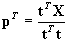and . Using the new value of p in an extra loop, we can then obtain the orthogonal values of the x-scores via .

Categorical Variables

Often we have to deal with variables that come in a discrete form. One example of such data is known as categorical, which does not lend itself to a natural ordering such as {1, 2, 3}, e.g., MALE and FEMALE or RED, GREEN, and YELLOW. Such variables can be represented using a 1-of-n coding scheme without imposing an artificial ordering. For example, if a variable consists of three categories - A, B, and C - then a natural representation of the variable would be (1, 0, 0), (0, 1, 0) and (0, 0, 1), depending on whether the outcome is A, B, or C, respectively. STATISTICA PLS uses this arrangement to represent categorical variables.

PLS for Classification Problems

STATISTICA PLS uses a 1-of-n coding scheme for handling categorical dependent variables. For a variable with n categories, n – 1 dummy variables are created, and the normalized outputs of the PLS model are interpreted as class membership probabilities (see the Categorical variables section above).

Variable Importance in the Projection (VIP)

In PLS models, a good indicator of a predictor's modeling power is VIP. The computation of VIP is similar to Power, except that the proportion of variability explained in the X variables is further weighted by variability accounted for by the components.

Variable importance in the projection (VIP) for variable j is given by:

where

N = number of predictors

k = number of PLS dimensions extracted

wcj = weight of variable j for PLS dimension c

SSc = explained sum of squares of the PLS dimension c

SSTotal =

Variables that have values of VIP larger than 1.0 are considered important.